nmr – Electronic Projects

31/05/202031/05/2020

Testing the RF coils

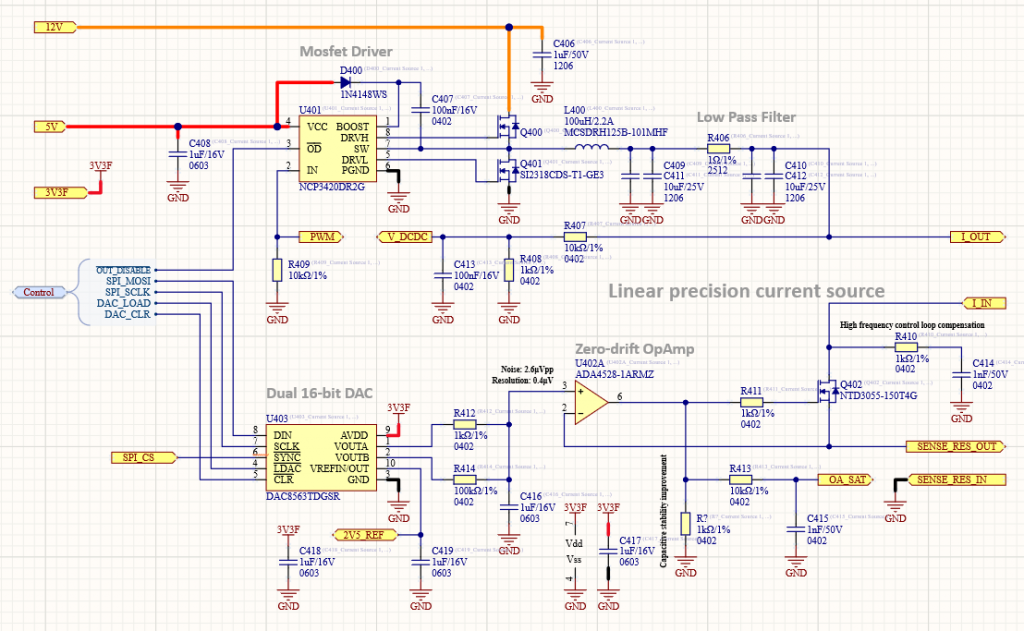
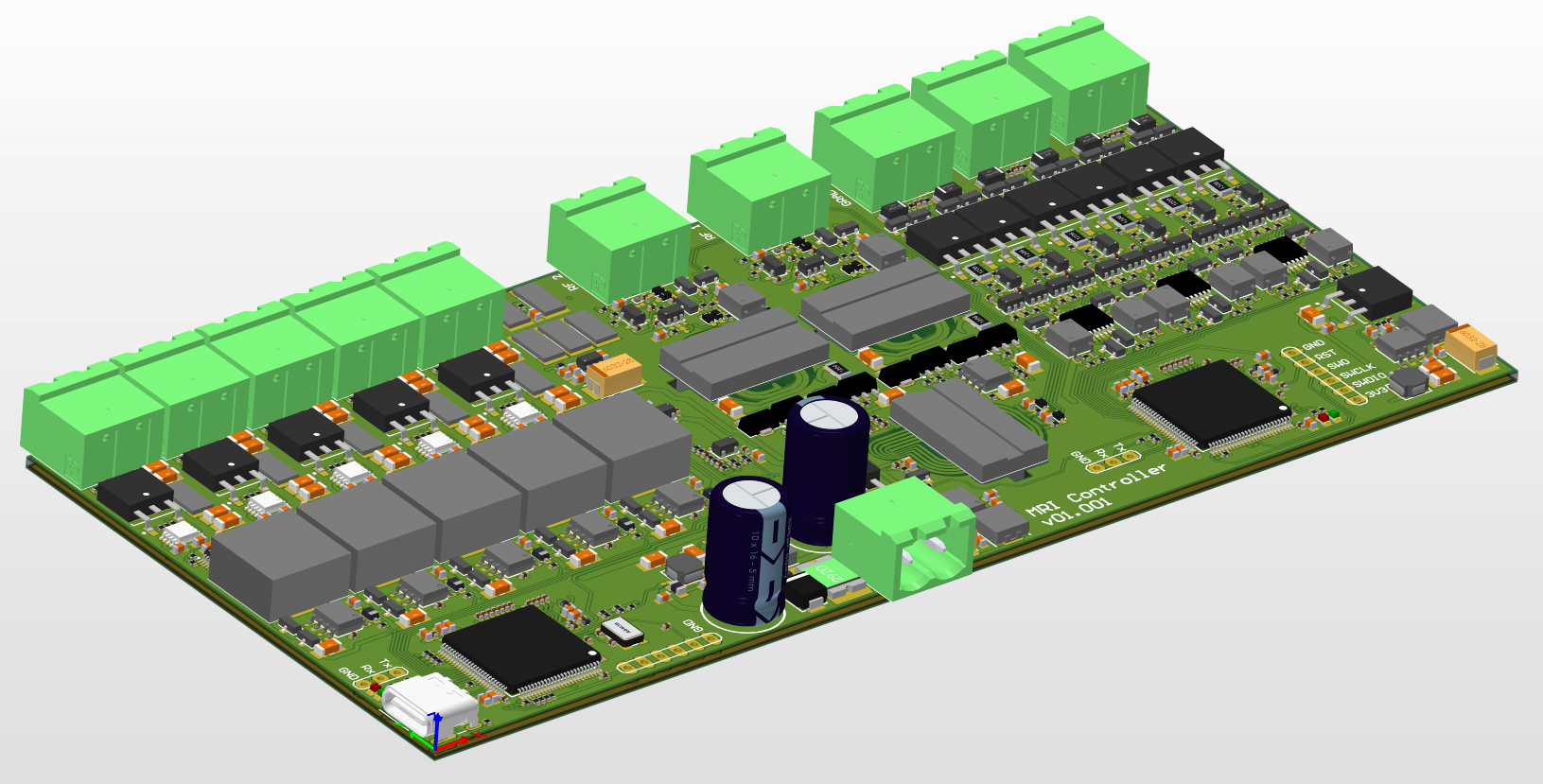
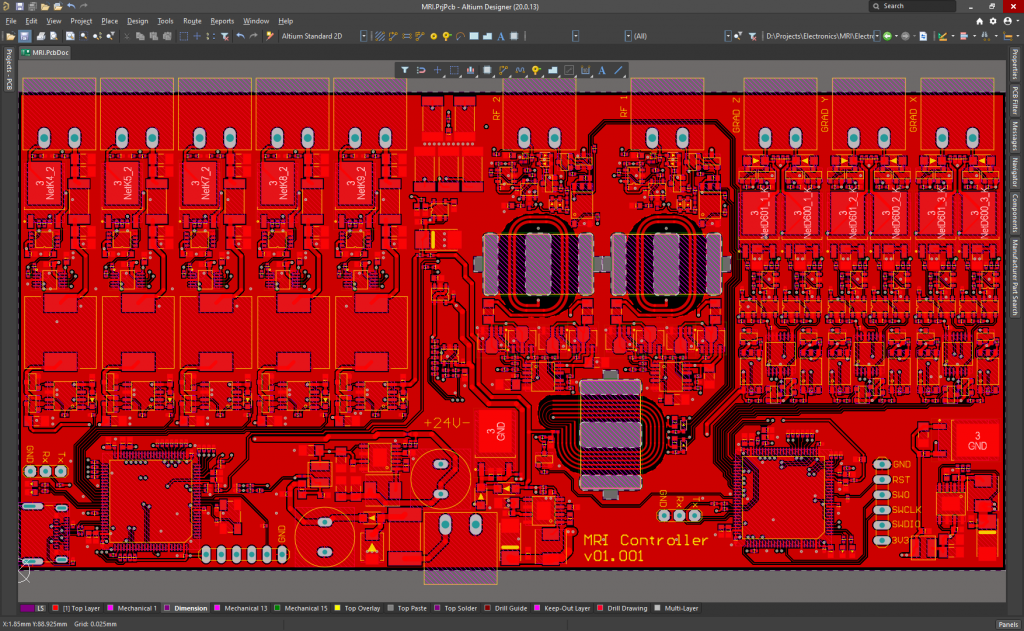
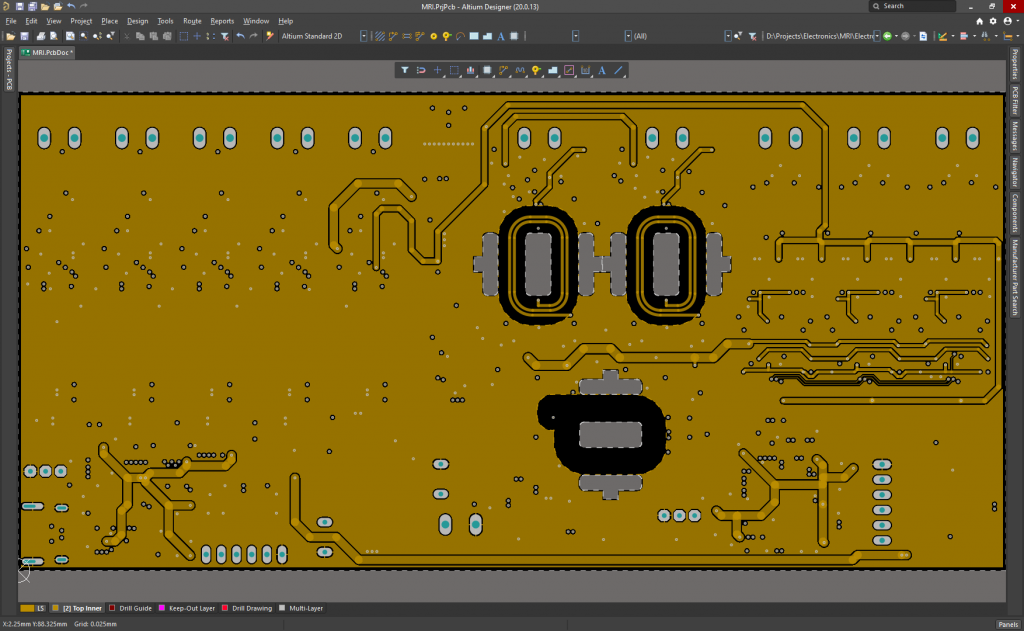
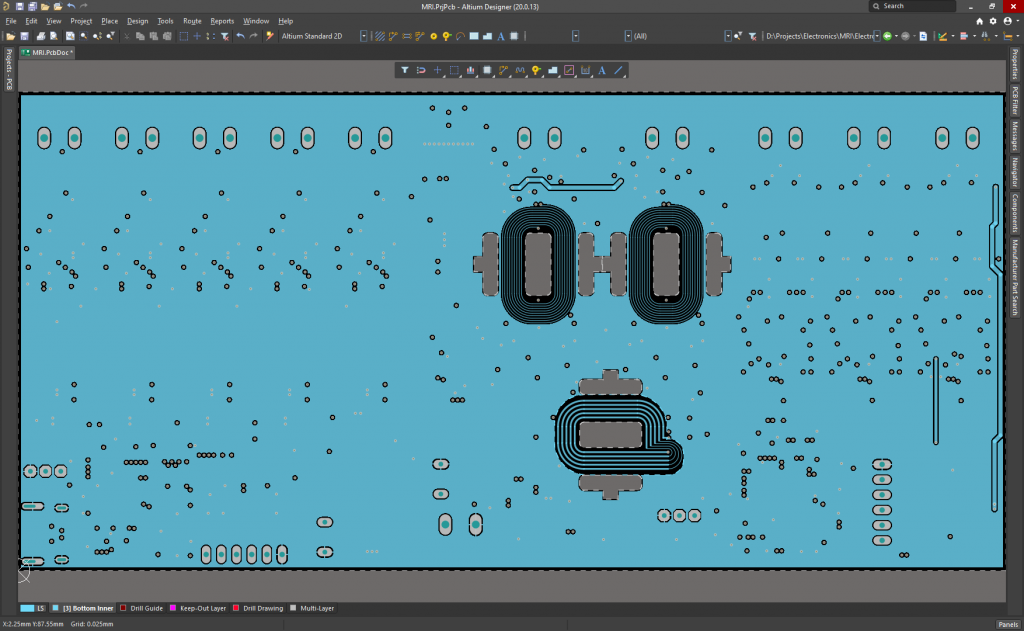
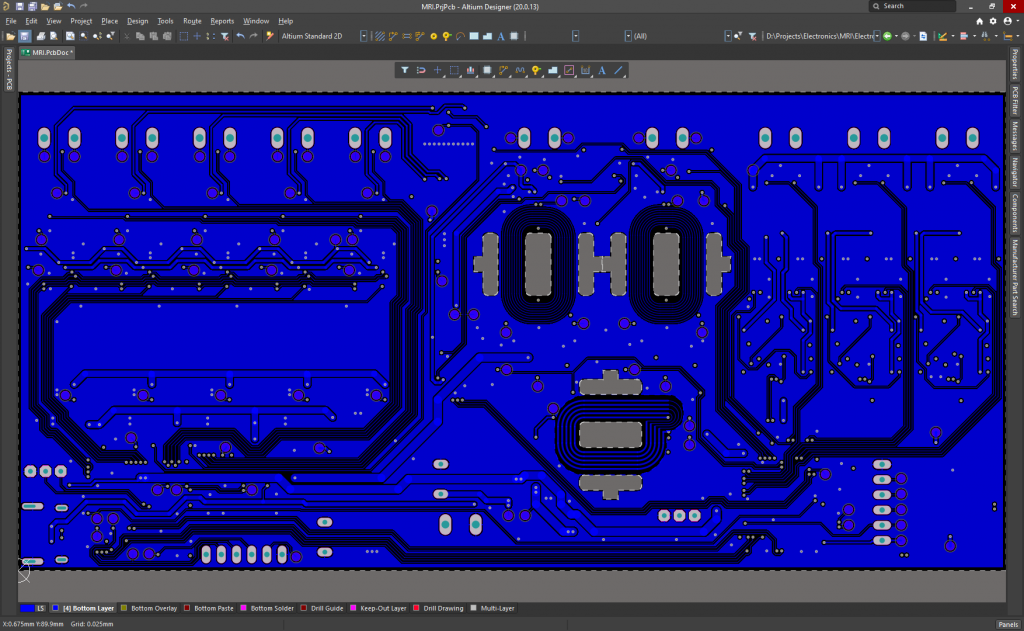
Since I still don’t have the quadrature differential amplifier assembled, I’ve tested a single coil pair (2 opposite side coils connected in series) using the function generator and the oscilloscope. Here the steps:

The coil pair is connected to the CH1 of the oscilloscope. The oscilloscope probe was set to 10x to reduce the stray capacitance, which now decreased to 13pF
A single turn copper wire loop with a diameter of 50mm was placed in the center of the RF coil structure. It was axially rotated until finding the maximum signal. In this position, if turned 90º, we would receive no signal (it would be received by the other coil pair)
Then, I’ve connected the output of the function generator directly to the previous copper wire loop. The output impedance of the function generator has a standard 50Ω impedance, and the copper wire loop, a short circuit. So, configuring the output with 1V square wave at 2kHz, the current to the single turn coil is 1V/50Ω=20mA. In this way, I’m generating a pulsed magnetic field, and thus I can see the output response of the coil pair

The single copper wire loop:

The setup:

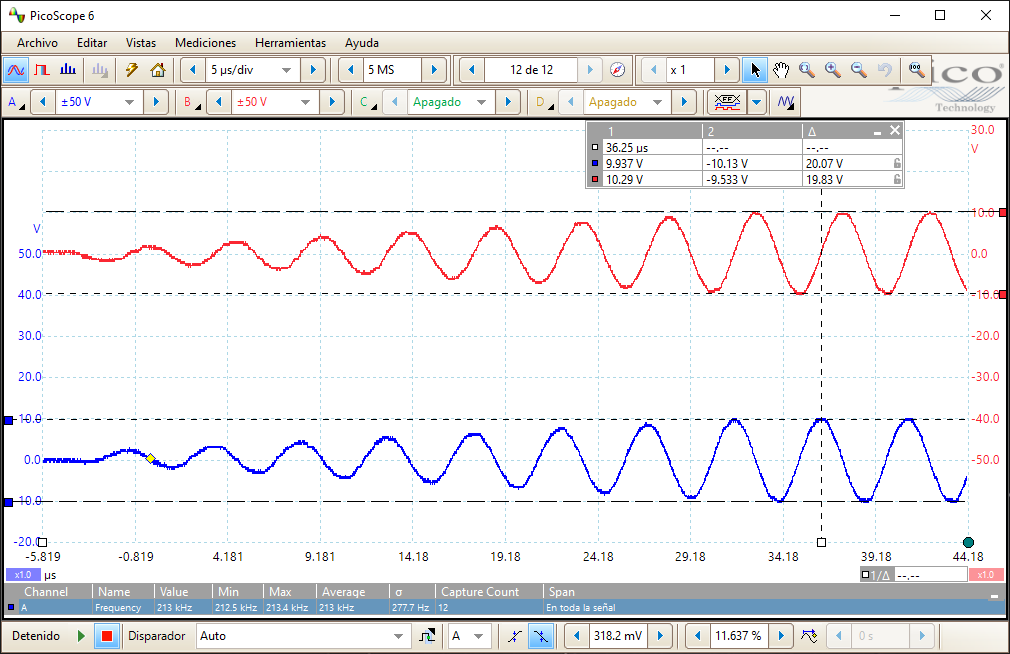
And finally, the output resonating signal:

I’ve added an external 100pF capacitor to tune to the desired 210kHz, which added to the probe capacitance of 13pF means a total of 113pF.

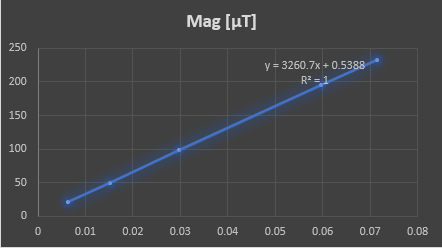
I calculated the generated magnetic field by using the single wire loop equation:

$\vec{B}=\frac{\mu_{0}I}{2R}\hat{j}=\frac{4\pi 10^{-7}0.02}{2\cdot 0.025}\hat{j}=0.5\mu T$

Here in Catalunya, we have an earth magnetic field of around 45μT, which means I’m generating a pulse about 90 times smaller. Despite this, we can see an output response of about 0.5V_PP. Not bad!

Q Factor

The theoretical values for the Q factor given the 2 measured coil parameters are:

Coil pair 1: 4.44mH and 16.8ohm. It means a Q Factor of 349 @ 210kHz
Coil pair 2: 4.48mH and 16.8ohm. It means a Q Factor of 351 @ 210kHz

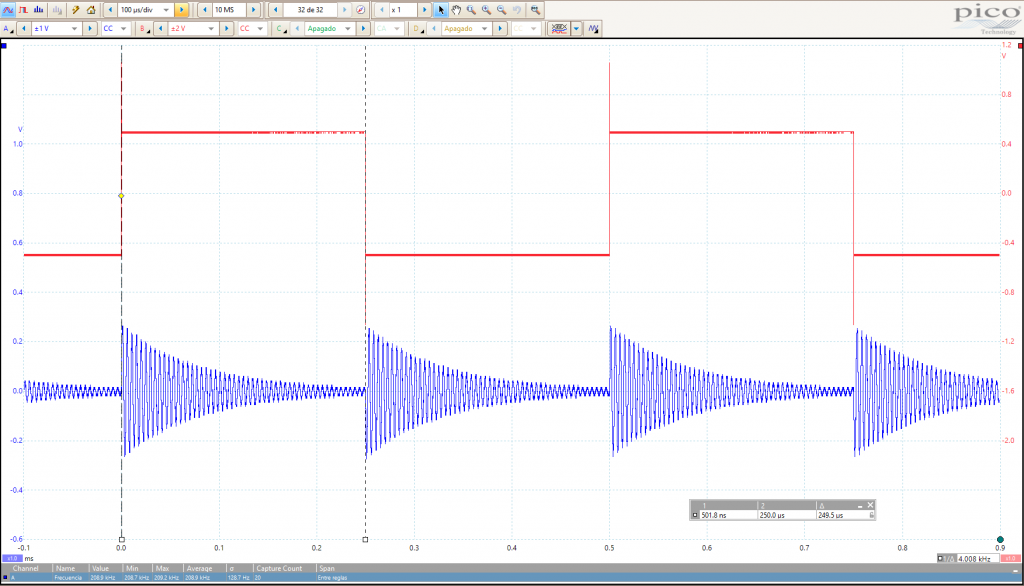
One way to measure the real Q is by using the resonating decaying signal. It consists of counting how many cycles it takes to reach half the initial voltage, and then, multiply that value by 4.53. Taken the previous acquisition, we see a Q=13·4.53=58, about 6 times lower than theoretically expected. In other words, the effective AC resistance became about 100Ω. The reason is the high frequency losses.

For such a “low” frequency and the wire diameter used, the skin effect is not a problem. But the proximity effect really is, where the magnetic field generated by the current flowing by the wire itself induces currents to the other adjacent wires.

For an unloaded RF coil (meaning there is no water sample), the Q factor usually goes from 50 to 600, while a loaded RF ranges from 10 to 100. So, we are in the worst-case range. The number of turns increases the proximity effect losses, although it also increases the sensitivity.

One might think that the highest the Q factor the better, because it is the ratio between the stored energy and the energy lost per cycle. But that’s not actually true, some NMR labs even intentionally decrease the Q by adding a series resistor. The thing is that the highest the Q factor, the sharper the frequency response, and the lowest the bandwidth. And we need some bandwidth to acquire the MRI signal when we apply the gradient magnetic fields.

The bandwidth can directly be calculated from the Q factor, but I wanted to measure it to make sure. So I swept a constant current sinusoidal signal through the single wire loop, and measured the RMS voltage at the output of the LC resonator. Here the result:

The orange trace shows the -3dB level, defined as the bandwidth threshold

In this case, there is no surprise and the theoretical value corresponds with the real one. The Q factor is defined as:

$Q=\frac{f_r}{BW}=\frac{212kHz}{4kHz}=53$

I don’t really know the NMR implications about not having a so high Q factor, but what I do know is that 4kHz of bandwidth is a perfect span for the gradient magnetic fields, as already seen in the next gradient section.

Finally, from the above plot we can directly get the sensitivity:

$Sensitivity=\frac{2.45V_{RMS}}{0.178\mu T_{RMS}}=13.78V/\mu T \, @ \, 212kHz$

03/06/202003/06/2020

Schematics, schematics, schematics…

Working hard on the electronic schematics these days! I’m done with the main B0 current source, finally with less than 3µV_PP of noise from 0.1 to 10Hz and 0.4µV of resolution. The voltage-to-current conversion will depend on the shunt resistor, where the worst case is when using a 0R47: the noise and resolution will be of 6µA_PP and 0.8µA. I need that much resolution to get the required magnetic field trimming.

I’m also using an NTC close to the current sense resistors, thermally coupled among them and chosen with the same size and PPM/ºC, to compensate by firmware the resistor variations due to self-heating.

I’m using a DC/DC controlled by the microcontroller to adjust the voltage in the MOSFET drain, and let it work in the linear region. I need the DC/DC because too much voltage across the MOSFET implies too much dissipated power. The main microcontroller will initially perform a calibration:

1. Set a current of let’s say 100mA using the 16-bit DAC
2. Start increasing the duty cycle of the PWM to rise the I_OUT voltage
3. While increasing, keep checking the OA_SAT pin. Right now it will be 3.3V because the small I_OUT voltage makes few current to flow through the coil, and the MOSFET will be in the saturation region. But when the OA_SAT pin becomes <3.3V will mean that we just left the saturation region, so we just need to increase about 0.5V more to give the MOSFET some margin to work properly in the ohmic region without dissipating too much power

A better way would be to connect the I_IN voltage to an ADC input, but it should have to be done through an operational amplifier with low bias current, or the shunt resistor would measure the sum of both currents and the precision would be lost.

A 100µH seems a pretty high value for the DC/DC, but we want the ripple current to be as low as possible. With a so large inductor, we don’t need large capacitors, but what is really important is that they have a low ESR, since that’s the main source of ripple noise. In this case, it’s MUCH better to have a total of 40µF using ceramic capacitors than 470µF using an electrolytic one.

Finally, about the high frequency control loop compensation network. It was added there because we are using a current source to control the current of a VERY large inductor (the one which generates the main B0 magnetic field). Without that network, the operational amplifier would be unstable and it would oscillate.

Let’s keep moving on!

22/07/202022/07/2020

Schematics finished!

It was hard, but the schematic is finally finished! Now I have to route the PCB, with a total of 722 components…

Still a lot of work to do, let’s see if I can finish it and get the PCB ordered before my holidays to assemble it then!

07/08/202013/08/2020

PCB finished and ordered

It took me about 2 weeks of work in my free time, but the PCB is finally finished! The main features:

5 independent channels of DCDC + linear current source to drive the 5 coils which generate the main B0 magnetic field. One 16-bit dual DAC per channel is used to configure the current setpoint, as well as generating an ultra-high precision 2.5V reference with low temperature drift and very low noise. Apart from using this reference for the current sources, the reference is spread through the board to be used as the main reference for the microcontroller’s ADCs, the signal amplifiers, the NTC sensor and the gradient coil drivers
2 independent drivers to generate the quadrature rotating magnetic field (RF field), as well as 2 amplifiers and all the logic to switch from transmitter to receiver. A third differential amplifier with some extra gain is used to remove the common mode noise and to acquire the NMR signal
3 independent drivers to generate the X, Y and Z gradient magnetic fields. The Z gradient field might not finally be used, since the simulations showed an homogeneity zone of just 1.5cm in the Z direction, but the driver will be there just in case

Two microcontrollers are used (STM32H7 family). The master is used to communicate with the computer through USB (USB 2.0 over a USB C connector) and to send commands to the slave. It also controls the PWMs of the 5 drivers to generate the B0 magnetic field, and to control each linear current source using each DAC (through SPI). It also measures the temperature using a NTC, thermally coupled to all the shunt resistors, and compensates the current setpoint when the shunt resistors temperature changes according to the temperature coefficient of each resistor, which was chosen as low as possible (100ppm/ºC).

The slave microcontroller is the one that performs the main MRI tasks. It generates both RF signals (the main and the 90º shifted one) using both internal DACs + DMA. It also controls the gradient magnetic field timings, and the integrated 16-bit ADC @ more than 5MSPS is used to capture the 210kHz signal.

PCB Layers:

It is powered at 24V, although the microcontrollers can run and be programmed using the 5V of the USB C connector when plugged to the PC. It measures 165.2mmx80mm, and it has been ordered to Eurocircuits today.

I will assemble it next week, I’ll post the results soon!

02/10/202002/10/2020

Project update

It’s been a while from my last post. I started a new small project to improve the cooling water system of my cutter laser device. The original 40W CO2 laser tube died, and I had to replace it. After some research I found out that the original system (water tank + pump) was not enough, since the water temperature must be regulated between 15 and 20 degrees, and the room temperature can reach to be as high as 30 degrees in summer. That’s why I used 2 water pumps with 2 different circuits, 4 peltiers (12V @ 15A), some temperature sensors, velocity controlled fans using PWM, heatsinks, a water radiator, a custom controller board to control everything, and all of crazy stuff. The thing is it is now working like a charm, and all the methacrylate pieces to build the MRI structure have already been cut.

I also did another small project with a digital magnetic angular sensor + ST eval board with a capacitive TFT display and TouchGFX, so that I can start winding the coils without loosing a single loop. Here a photo of the setup:

Once I get all the coils winded and assembled to the main structure, I’ll come back with more news 🙂

08/02/202108/02/2021

Measurement of the RF pulse signal

The initial design with the PCB planar transformer gave quite bad results in terms of signal distortion. That’s why I decided to use one pulse transformer per quadrature channel.

This transformer is a 1:1:1 (meaning it has 3 independent and equal coils). I use the first coil to apply the signal, and connecting the other two in series I get an output voltage 2 times higher than the input.

The signal applied to the trasformer comes from an operational amplifier working at 24V, with a maximum output voltage span of about 2V to 22V. I use 2 operational amplifiers to transform the single DAC output voltage (from 0 to 2.5V) to a differential voltage of ±20V. With the extra 2x gain of the transformer, we get a total output voltage of 80V_PP which can be directly applied to the RF coils.

Final desing with two VTX-110-006 pulse transformers

Mesurement of the static RF coil magnetic field

To calculate the flip angle given by the RF pulse, we first must know the magnetic field generated by the RF coils (which using the common nomenclature, we will call B1). So I used a digital magnetometer. I know it’s not the most accurate way to do it, but it’s a good starting point. Once I get some NMR signal, we will be able to play with the flip angle to find the optimum value.

The magnetometer was placed in the middle of the RF coil. I used a STM32 eval board to get the magnetometer data using I2C, and send it to the PC using a USB VCP. Then I applied some different currents to the coil to get this table:

I_DC [A]	Mag [µT]
0.00637	21
0.0152	50
0.0298	98
0.0595	195
0.0714	233

Now we just need to know the impedance of the coil at the NMR frequency. It’s important to measure it instead of just calculating it, because we also want to have into account the high frequency loses (like the proximity effect one). So I used a 216Ω shunt resistor to measure the current with the oscilloscope, and I applied 8.6V_PP with the function generator. A simple V/I division gives an impedance of 6435Ω @ 213kHz.

Flip angle and flip time

The flip angle just depends on the time we apply the pulse and the magnitude of the applied magnetic field (B1). Here the equation:

$PulseTime=\frac{DesiredAngle}{360 \cdot LarmorFrequency \cdot B1}$

Knowing that we can generate up to 80V_PP, we can get the current of the coil from the previous calculated parameters:

$MaxCoilCurrent=\frac{80V_{PP}}{6435\Omega}=12.4mA_{PP}$

Now, from the tendency line equation found out in the previous plot, we can find out the B1:

$B1=3260.7 \cdot 12.4mA_{PP}+0.5388=41\mu T_{PP}=20.5\mu T_{P}$

We now will use the peak magnitude instead of the peak to peak. It is clear why when we apply the common trick of switching to the rotating frame of reference, so that we now rotate with the nucleus and see a static magnetic field. The quadrature system with a sine/cosine signal will make that the nucleus sees a static and constant magnetic field with a magnitude equal to the peak value.

Note that to flip the spin angle to 90 degrees we are talking of only 20μT! This result was quite shocking to me, since it’s about half the earth magnetic field! I didn’t expect that…

Now we have all we need to calculate the flip time to get a 90 degree flip angle:

$PulseTime=\frac{90}{360 \cdot 42.58MHz/T \cdot 20.5\mu T} = 285\mu s$

This time is equivalent to:

$213kHz \cdot 285\mu s=61 sinusoidal\ cycles$

Quadrature signal

Here I show the oscilloscope capture of the 2 signals which are applied to the RF coils. They are generated with the internal DAC peripheral of the microcontroller, a DAC configured in dual mode (both channels updated at the same time) to send the signal to each channel. It’s actually the same signal, but shifted 90º to give the quadrature feature.

The signal shape is first calculated using a “for” loop, and stored in a RAM array. Then, using a timer, each data in the RAM array is transferred to the DAC using a DMA. The resultant signal is very smooth, since I’m running the DAC at 5MSPS to generate the 213kHz. All this process is already generated inside the microcontroller, but I have some programming work to do to control everything from the computer.