The RF coils design is also one of the main essential parts to get a decent result. By means of these coils we will excite the spins, as well as read the signal back.
First of all clarify the term “RF”, since it might cause confusion. We are not dealing with electromagnetism or radio-frequency here, just with the same kind of magnetism found in a magnet. This term is just used for historical reasons.
We already saw the main magnetic field B0 homogeneity is crucial to get some signal, but the magnetic field generated by the RF coils must also be as homogeneous as possible (not in the parts-per-million range though). The reason has to do with the flip angle, as explained below.
RF magnetic field homogeneity
As you probably know, the spins will flip its angle depending on the strength of the applied magnetic field as well as the excitation time. For example, if your spins flip 90 degrees by applying a magnetic field of B µT for t ms, you will get the same 90 degrees flip angle by applying a magnetic field of 2·B for t/2.
The whole sample is exposed to the generated magnetic field for the same amount of time, so I guess you see the problem: if for the same time t some volume in our sample is exposed to twice the magnetic field strength, instead of flipping the spins 90º they will flip 180º, and we will receive no signal at all from that volume.
Clinical MRI usually uses birdcage coils. That’s because, at 1.5T and 64MHz, the LC resonant frequency is so high that the inductance must be quite low. As low as the inductance of a single loop of wire. And it’s not helping that the geometry has to be very large to fit a human being inside, since the higher the loop area, the higher the inductance. Sometimes, the single loop is even split into smaller loops by adding capacitors in series.
Fortunately for us, we are not working at such high frequencies nor volumes. At 5mT and a resonant frequency of about 210kHz, our inductance can be much larger. Furthermore, the smaller volume also allows us to get a smaller coil, which means we can increase the number of turns. In fact, we want to have as many turns as possible in order to get as much signal as we can, as already described in Faraday’s law of induction.
Because of its well-know homogeneity, I will use a saddle coil geometry approach. Furthermore, since we are dealing with a rotating magnetic field, I will use 2 of them in quadrature, which will give us some SNR improvement. There are two factors in this SNR improvement:
1) Having more coil turns means having more signal
2) We are dealing with a non-shielded design with some external noise coupled to the coils. So the idea is to use the quadrature to get a differential signal, in this way all the common mode noise will be canceled out
This last idea is shown here:
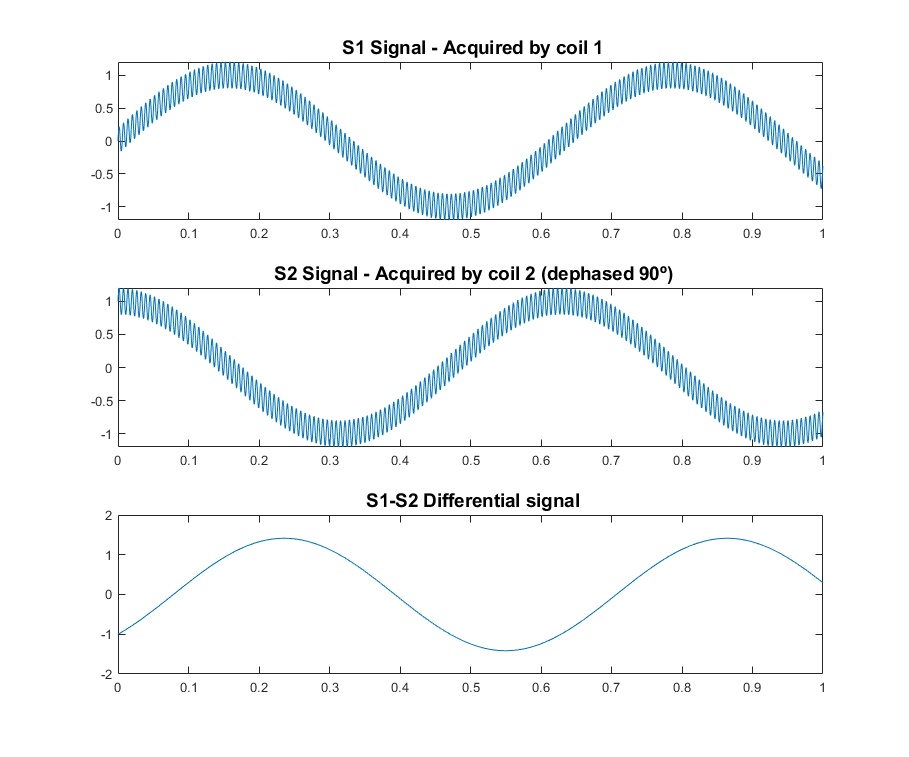
In both S1 and S2 signals the external noise is the same, that’s why when subtracted we get rid of it. We are not canceling out the NMR signal though, because the coils are oriented with an angle of 90º, which means we will get a sine in S1 and a cosine in S2. In other words, the resultant signal S1-S2 will be 
.
In order to totally cancel the noise out, the problem is that the external noise must be exactly coupled to all the coils. But it’s not possible with the saddle coil geometry, because it would imply to have one coil pair larger in diameter than the other one; otherwise, they would physically overlap. And having a larger coil means more area, which in turn means more external induced noise in that coil. Furthermore, it’s also important to have the same coil parameters for all of them, like inductance, series equivalent resistance, and stray capacitance. In other words, the Q factor and the self-resonant frequency. Well, everything invites us to make a design as symmetric as possible, regardless of the saddle approach. I’m going to use a modified one, like the one you can see here:
This is nice, because all the four coils are exactly the same now. The drawback is that the geometry is different, and so we have to run some more simulations to figure out what’s going on.
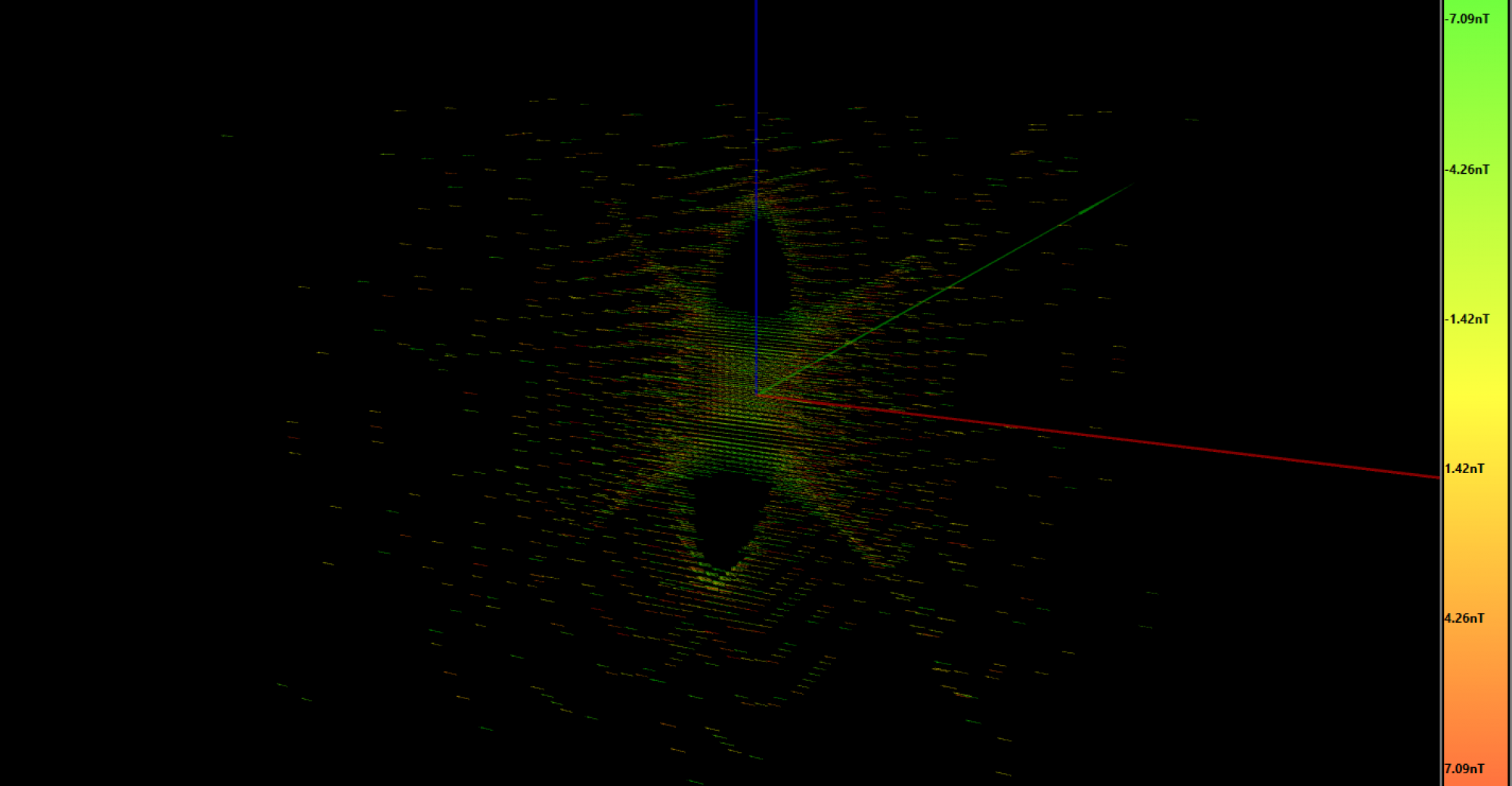
In order to achieve the best homogeneity, the saddle coil geometry is defined to have 120º between arms of the same coil with respect to the axis. To figure out which angle is the optimum one for our modified design, I’m going to sweep the saddle angle while monitoring the resultant total homogeneity using my C# program simulator. I modeled the coil geometry programmatically, because it would take me a lot of time to write another software to translate a 3D model to a list of 3D vectors used in my software. The nice thing doing it this way is that I also could program the coil geometry parameters, like the angle to sweep, which wouldn’t be possible using a “static” model approach (e.g. like importing an STL). Here I show the results:
And the same simulation looking from the side view:
It’s interesting to see how the homogeneity peaks at 142º. We have our magic angle, and it’s not 1.1º like the graphene one! 😛
Since I’ve come this far, I wanted to make one last simulation. The previous simulations show the homogeneity at 0º or 180º, but not with both coil pair working together in any angle, which is our real case when we get the rotating magnetic field. That’s what is shown in that last simulation:
At the bottom-left side you can see how the homogeneity fluctuates over time. The magnetic field is only constant at the central point, so, for a real and accurate result, I should have integrated each voxel with the exposed magnetic field over one entire turn. That’s how I would know the total energy received by each water molecule and so the real flip angle. Despite this, I didn’t want to waste more time here since I see quite good results in the central slice. Furthermore, I wouldn’t know how to improve this design further, I’ve done my best at this point.
I haven’t mention it, but I’ve dimensioned the coils to have a diameter as small as possible, but containing as much as B0 homogeneous magnetic field as possible. That’s how I pretend to get a maximum filling factor.
Mechanical design
Once the coil geometry is clear, I’ve designed the custom coil former, which I 3D printed. Here you can see a 3D render animation:
This design makes the coil winding process quite hard and slow, because of its closed design which forces me to wind it like a toroid inductor. Furthermore, after winding one coil, I saw it was difficult to get a good symmetry, because of the half-open concept which keeps one sector more squeezed than the other. That’s why I designed a more sophisticated system, where each coil can be wound individually, and then fixed altogether using nylon screws:
Which is the composition of 4 exactly equal and symmetric coil formers like this one:
Electrical parameters
I wound a single coil to get a rough idea of the coil’s main parameters. The thing is that I could calculate the resultant inductance and series resistance using the Solidworks plugin, which gives you that information taking into account the coil geometry, number of turns, and wire diameter. But I couldn’t get the stray capacitance, which I have no means/knowledge to calculate it. Furthermore, it’s very dependent on the way the coil is wound: it’s not the same to have some overall initial coil section overlapped with some final section, than to have a perfect wound vertical section for each turn around the whole coil. After winding one coil I saw it’s hard to get that perfect vertical section, because the radial force toward the center in the curved plane makes that the wires spread on the surface. That’s why in my redesign I’ve given a bit more space in the axial direction. Now the coil should fit much better without overlapping at the final turns, and now I clearly see it’s almost impossible to calculate the stray capacitance.
That stray capacitance is a very important factor because, together with the coil inductance, it produces a self-resonant frequency. If that self-resonance is close to the nuclear magnetic resonance, we will have no room for the input impedance of our signal amplifier. The worst-case would be that the self-resonance became lower than the NMR frequency, in this case we could get no measure at all.
Summarizing: given a maximum copper volume defined for our coil former, this design is a trade-off between self-capacitance and series resistance while trying to keep the maximum number of turns.
I used 110 turns of 2x 0.2mmØ joined together. The thing is I needed 0.3mm copper wire but I didn’t have any reel available. Just mention that at 210kHz the skin effect for a 0.3mmØ wire begins to be perceptible, but not enough to justify the use of Litz wire. I used my NanoVNA device to get the parameters:
Which in this setup are:
- Resonant frequency: 715kHz
- Inductance: 1.5mH
- Stray capacitance: 33pF
- Series resistance: 7ohm
This is not the exact final design, but it is telling me I’m on the right way. Given the previous parameters, the Q factor at 210kHz is 283, quite good! 🙂 Putting it all together, my conclusion is that I will use few more turns when winding the 0.3mmØ copper wire in my final coil former. Adding more turns will increase the Q factor because the inductance increases quadratically with the number of turns while the resistance only linearly. But the self-resonant frequency will be lowered at a much faster rate as well, since apart from the inductance, also the stray capacitance increases. As far as we keep the self-resonant frequency with a good margin above the desired NMR frequency, we should wind as many turns as possible to maximize the NMR signal.
Another useful parameter derived from the above data is the 
of our air core coil former, which is of about 
. So I can calculate the inductance for any number of turns, e.g. for 130 turns, 
. In this last case, the resistance would increase from 7Ω to 8.7Ω, but the Q factor would increase from 283 to 318. I have no idea about the stray capacitance in this new case, but supposing no capacitance variation, we would have a self-resonant frequency of about 600kHz (which will be lower due to the real higher stray-capacitance). I guess I will try with about 150 turns if the coil former allows me to fit all of them.
More results coming soon!