This is one of the most important and complex parts in the design, and it happens to be the first one to deal with. That’s because all the rest of the design constraints will be based on the result of this one. Three parameters are the most important ones:
1) Magnetic field strength: Through the gyromagnetic ratio of the hydrogen (42.58MHz/T), the magnitude of this main magnetic field will directly give us the resonant frequency of our spins (also called the Larmor frequency), and so, a great part of the electronics design. Furthermore, for higher magnetic field strengths, not only the frequency is higher, but the amplitude as well. After the simulations, I can anticipate that the coils will generate 5mT. At such a low field, we are speaking of 5mT*42MHz/T= 210kHz. Very low compared with a real MRI with 1.5T and 64MHz… Let’s see what we can do with that
2) Magnetic homogeneity: It’s one of the most important issues, and where I spent most of my time with simulations. If you imagine the whole water sample as the sum of small water volumes, having a low homogeneous magnetic field means that each of them will see a different magnetic field strength, and so, they will resonate at a slightly different frequency. It means that after the generation of the RF pulse to synchronize all the spins, the phase among the spins will gradually be lost, as well as the signal to measure. In a high strength magnetic field this wouldn’t be so dramatic, since the resonant frequency would be much higher, and for the same inhomogeneity and amount of time, we would have many more cycles to acquire the signal. But that’s not our case, complexity is growing!
3) Effective volume: Unfortunately, there is no way to make a perfect straight magnetic field line in the real world. So, we can define the effective volume as the volume where the magnetic field is constant enough to get the required small spin dephasing which allows us to measure the signal. As I will explain later, I found a method to achieve a magnetic field lower than 10ppm over several cm3 of volume (at least in theory). The effective volume is important because it will give us the constraints for the RF coil geometry. In order to get a high filling factor and as much SNR as possible, it should cover as much effective volume as possible, and at the same time, cover the maximum water sample volume as possible.
In order to generate high homogeneous magnetic fields, the way to go is using coils. Maybe in a few years we will have available some nice graphene room temperature superconducting wires hehe But until then, we have no other choice but to deal with copper.
There are some standard geometries already known to get highly homogeneous magnetic fields, like the Helmholtz coils. But for our purpose, I want a coil which performs a better job. The first thing I did was programming a Visual Studio software (C# is my preferred high-level language) to simulate magnetic fields given any conductor shape based on the Biot-Savart law. The main idea was to use my custom software to design the main structure, but the 3D calculations were so CPU demanding that I had to find another approach. Once the CPU calculations are done, WPF is great, since it uses the GPU to render the graphics. Now I just use this software to validate and observe the final result, to design the main structure I finally used Matlab.
I use a Solidworks plugin to simulate magnetic fields, but just to get a rough idea. We are dealing with ridiculously tiny scales here. For example, 10ppm of 5mT results in a magnetic field variability of 50nT, 1200 times weaker than the earth’s magnetic field. At this point, these kinds of software which use a solid mesh approach are not precise enough. Furthermore, you can’t process the data results in a custom manner.
Matlab script
As well as I did in my custom C# software, I implemented the discrete Biot-Savart law to calculate the final resultant magnetic field. Despite this, they were coded a bit different:
In C#, I calculate all the 3D magnetic vectors in each volume point, having into account all the defined objects carrying some current. So, it is the most generic version of the Biot-Savart equation
In Matlab, I coded a specific case of the generic equation, the case where we have loops of wires. So, a first step calculates the magnetic field along the central X-axis given the 
position, the radius, and the current I. Then, we iterate for each defined loop wire (with different and radius) to integrate the final resultant magnetic field. But just along the X-axis. That’s why I will use the C# software to visualize the resultant 3D field of the entire structure once it is defined using this script
That’s how it works:
function [x,B,R,P,len,kg] = CalculateMagneticField(Winding, Radius_mm, I, wireDiameter_mm)
Winding: A matrix of [N, X] elements. Each matrix value can be 0 or 1, depending on the coil being populated with copper wire or not. The X position multiplied by wireDiameter_mm/2 gives the distance along the wires:
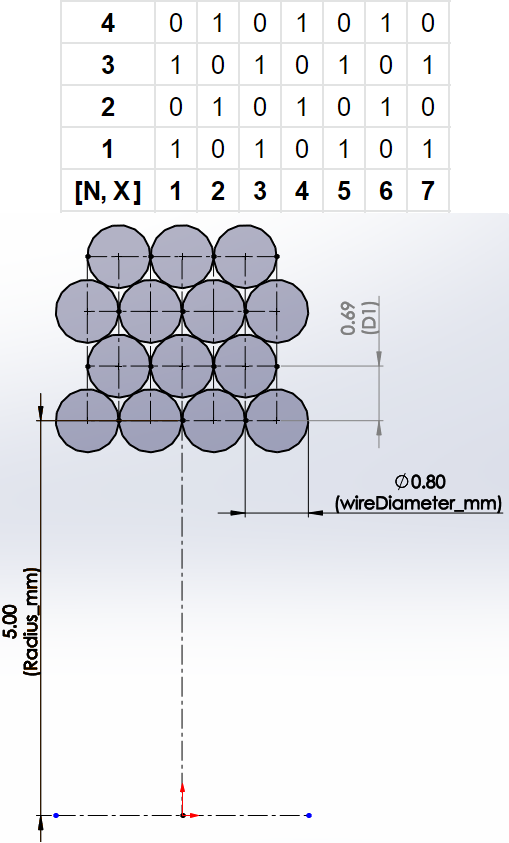
Radius_mm: The radius of the first layer from the central axis. The rest of the radii are automatically calculated having into account we are using round-shaped wires. The image above shows how the vertical distance is lower than the wire diameter. Simple trigonometry shows the fitting factor is wireDiameter_mm·cos(30). Despite this, since the coil is wound back and forth and the spiral will change the direction in each new layer, the radius will vary from wireDiameter_mm·cos(30) to wireDiameter_mm, depending on the turn angle. In fact, it will have 2 maximum and 2 minimum peaks per turn, fluctuating at each 90º. It means that, if perfectly wound, it would create an elliptical shape if lots of turns were required. But we live in a non-ideal world, and the coil former width will not mathematically be as designed. So each time we reach the end of the coil former and the spiral changes in direction, the angle will randomly dephase a bit. These cumulative errors make us a favor, and so I will use the average as an effective fitting factor: 
I: The current of the whole winding
wireDiameter_mm: Just comment that I used a fitting factor outside this function, so, instead of using 0.8mm for a 0.8mm diameter wire, I will use 0.86mm for imperfections when winding
Then, it returns:
x: A vector, where each element contains the position of each calculated magnetic field B, with 0mm located at half the vector. Its length equals the X size of the winding matrix
B: A vector with the resultant magnetic field, corresponding with the previous distances
R: Total resistance of the resultant coil
P: Total power dissipated by the coil, given the current I and the previous calculated R
len: Total copper wire length to wind this coil
kg: The total copper weight
After coding this function, I tried to use a solver to maximize the homogeneity, but it’s a complex function to solve. It couldn’t converge, or converge at non maximized solution (I tried with the simple Helmholtz coil). So, I just did it myself. I programmed a second script which will call the previous one to act as a tool to make this coil design process easier for me. I empirically started with 1 central winding of X turns and N layers per turn. Then, modifying X and N, as well as the radius, I could observe how the final resulting magnetic field changed along the central X-axis. At this point I was watching myself as an IA network training myself hahaha Here I show this script in action:
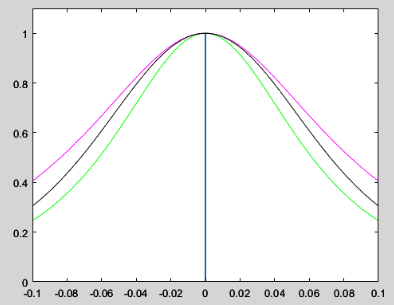
In green, I show the magnetic field for a 1 single loop wire. In pink, a 100 turns coil organized in 100 layers (multi-layer, thin coil). And finally in black, also 100 turns but organized in 1 single layer (single layer, wide coil). As you can see I show the unitary magnetic field, of course a 100 layer coil generates a much higher magnetic field than a single layer. But the scale can be changed by changing the current, on the other hand the shape of the magnetic field can not be adjusted and just depends on the geometry.
To get the most homogeneous magnetic field, we need to get a straight line at the center, where we now see a curved shape. As you can see, we need to form a straight line adding curves.
Here I configured the script to plot a Helmholtz coil. I set a radius of 70mm and, as the geometry requires, a separation between coils of 35mm (radius/2). Each coil formed by just 3 wires of 1mm of diameter:
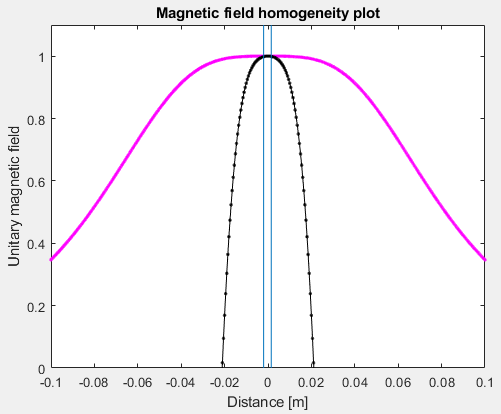
The 2 vertical blue lines show the zone where the homogeneity is lower than 10ppm of the central magnetic field. In this case, 3.5mm. The pink line is the total unitary result, and the black line is the vertical unitary zoom of the pink line (amplified about 5000 times). In this way, if I separate a bit both coils, we can observe the effect in the black line but not in the pink one:
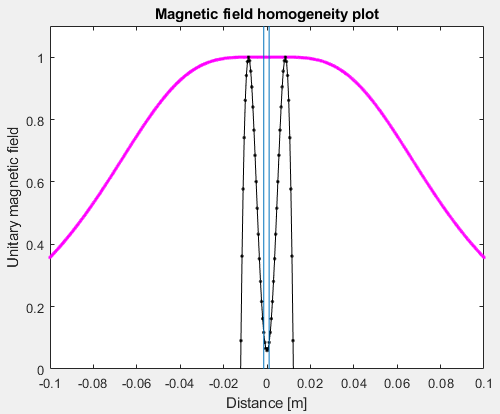
Separating the coil 2mm from each other, the homogeneity zone is decreased to 2.5mm. The black line shows the effect of the coil separation, which is weakest now at the center.
Seeing the above image, I thought the way to make a more homogeneous magnetic field was separating even more both coils, and adding an extra central coil, where the central peak would add to the central notch and make it more straight. After that step, I saw that adding a second couple of coils (a total of 5 now) would improve a bit more the homogeneity. Despite this, adding more coils was not effective for the size I was dealing with. The peaks are too broad and overlap too much with each other. Here I plot the final result after lots of iterations:
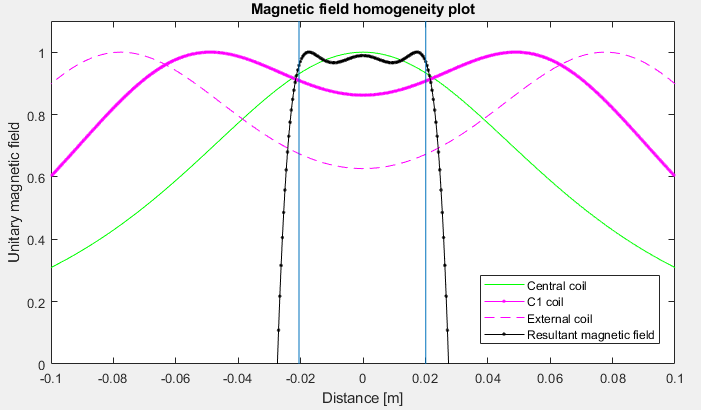
The black line now, apart from the zoom, is also the sum of all the 3 magnetic fields, generated by the central coil, and the 2 pairs of extra coils. I used the black line to know where the magnetic field was too weak or too strong, then I could adjust the adjacent turn wires and current to make the center as flat as possible. With this solution, the homogeneous magnetic field zone increases up to 34mm, with 4ppm from the central 5mT. This means we have a magnetic field of 5mT ± 10nT! Great 🙂
I could even get a flatter response, it is a trade-off which reduces the homogeneous zone.
The way to calculate the number of turns and geometry was iterating, knowing the effects that have adding layers or making the coil wider, as seen before in the first script example. I could also play with the currents to increase the magnetic field of each pair of coils when I didn’t want to increase the number of turns (but having into account that I want the same dissipated power in each coil). After some time playing with the script, I started to see some patterns and what to do to make the lobes flatter. The results of the script:
Central Magnetic field: 5.001 mT
Larmor freq: 212.9443 kHz
Total Power: 8.407W
Homogeneous space: 34mm
Copper weigth: 6.7249kg
Furthermore, the script writes a text file with the dimensions of the coils, in a format that Solidworks can understand using the equation editor. In this way, just executing the script, Solidworks can update the shape of the final result, which you can see here:
The results for each individual coil, with a copper wire diameter of 0.86mm:
Central Coil:
CC Current= 303.5134 mA
CC Coil Turns= 1125
CC Total R= 20.8815 ohm
CC Wire Length= 641.1368 m
CC Coil Weight= 3.0337 kg
CC Voltage= 6.3378 V
CC Power= 1.9236 W
C1 Coils:
Displacement from center=±54.12mm
C1 Current= 628.7246 mA
C1 Coil Turns (1/2)= 204
C1 Total R (1/2)= 3.0428 ohm
C1 Wire Length (1/2)= 93.4263 m
C1 Coil Weight (1/2)= 0.4421 kg
C1 Voltage (1/2)= 1.9131 V
C1 Power (1/2)= 1.2028 W
External coils:
Displacement from center=±79.54mm
CE Current= 459.3984 mA
CE Coil Turns (1/2)= 585
CE Total R (1/2)= 9.6607 ohm
CE Wire Length (1/2)= 296.6185 m
CE Coil Weight (1/2)= 1.4035 kg
CE Voltage (1/2)= 4.4381 V
CE Power (1/2)= 2.0389 W
T2* due to the homogeneity
I’ve said that 4ppm is good enough, but I want to demonstrate it in numbers. At 5mT, the Larmour frequency is 212.9kHz. Since that frequency is proportional to the magnetic field, we can calculate the 4ppm over the frequency, which gives 212.9kHz±0.85Hz. In other words, the most dephased spins will take about 1.2 seconds to dephase 360º. I will use 90º of dephasing for this calculation since it’s a good approach to the time constant 𝜏 (usually 67%), and so our T2* would be of 90º/360·1.2s= 300ms. This is good! A T2 for water is usually in the order of 1.5 seconds. It has no sense to make more accurate numbers here since this will differ in reality, too many factors in real life, this was a rough approximation.
Of course, I have my concerns about achieving 4ppm, which are theoretical values given a perfect geometry. Furthermore, all these calculations were done with a relative permeability of copper = 1, the same as air, but in reality copper is a bit diamagnetic. And with “a bit” I mean 
. The error is in the order of some few ppm, so I guess we will be able to shim it using tiny current variations in each coil, the thing is the calculations would be too complex having into account this effect.
An advantage of this design is that I will use 5 different current sources, one for each coil, to shim the magnetic field. I will only be able to shim it in the Z direction though.
The earth’s magnetic field will also add up to our generated 
. We are talking about 1.2% of our 5mT. As seen in the Terranova device, they use shimming to improve the earth’s magnetic field. In our case, we will also have the 1.2% of the earth’s magnetic field inhomogeneities, which will fall into the sub-ppm region having into account we also have a smaller volume (if we don’t have any magnetic object close enough, of course). Despite this, the effect we might observe is a small shift in the expected final resonance, for example 212.52kHz instead of 210kHz (1.2%), but it can be adjusted with the shimming currents easily. Apart from this, I don’t know of any other external magnetic field which can affect us, just small misalignments between the 5 coils. I’m thinking about using some kind of hardware fine trimming for moving the external coils in small amounts, but some simulations showed that an error smaller than 1mm can be fixed adjusting the currents in each coil wire.
Another factor of a MAJOR consideration, even supposing we achieve a perfect and ideal copper winding structure, is the resolution of our current sources. The numbers are frightening and another challenge to overcome. As an example, our central coil runs at about 0.3A. If we want to be able to shim the magnetic field in 1ppm, we are talking about controlling 0.3μA! That’s insane… Some years ago I designed an EEG, so I can tell you that here we are dealing in the same order of magnitude than the signals generated by the brain on the surface of the scalp, with the aggravating that our full-scale is WAY larger.
One thing in our favor is that these huge coils with so many turns have a large inductance, which is good to keep the currents constant even using a DCDC. But the DC stability is what seems more difficult to solve. That’s because the spin-echo only works if the magnetic field is constant from the 90º pulse to the TE time, otherwise, the frequencies varies a bit and the 180º effect doesn’t compensate the inhomogeneities. The water itself is proportional to the resonant frequency, so we could use this fact as feedback to adjust the overall coils current, but this can only be done at the time we acquired the signal, not between pulses.
Lots of things will have to be taken into account, like the very-small resistance changes of our shunt resistors due to the temperature heating effect (which might be huge when talking about μA), the problem of voltage offsets drift in our amplifiers, ADC non-linearities, etc. I will show the numbers when I write that section.
Magnetic field simulation using the custom C# software
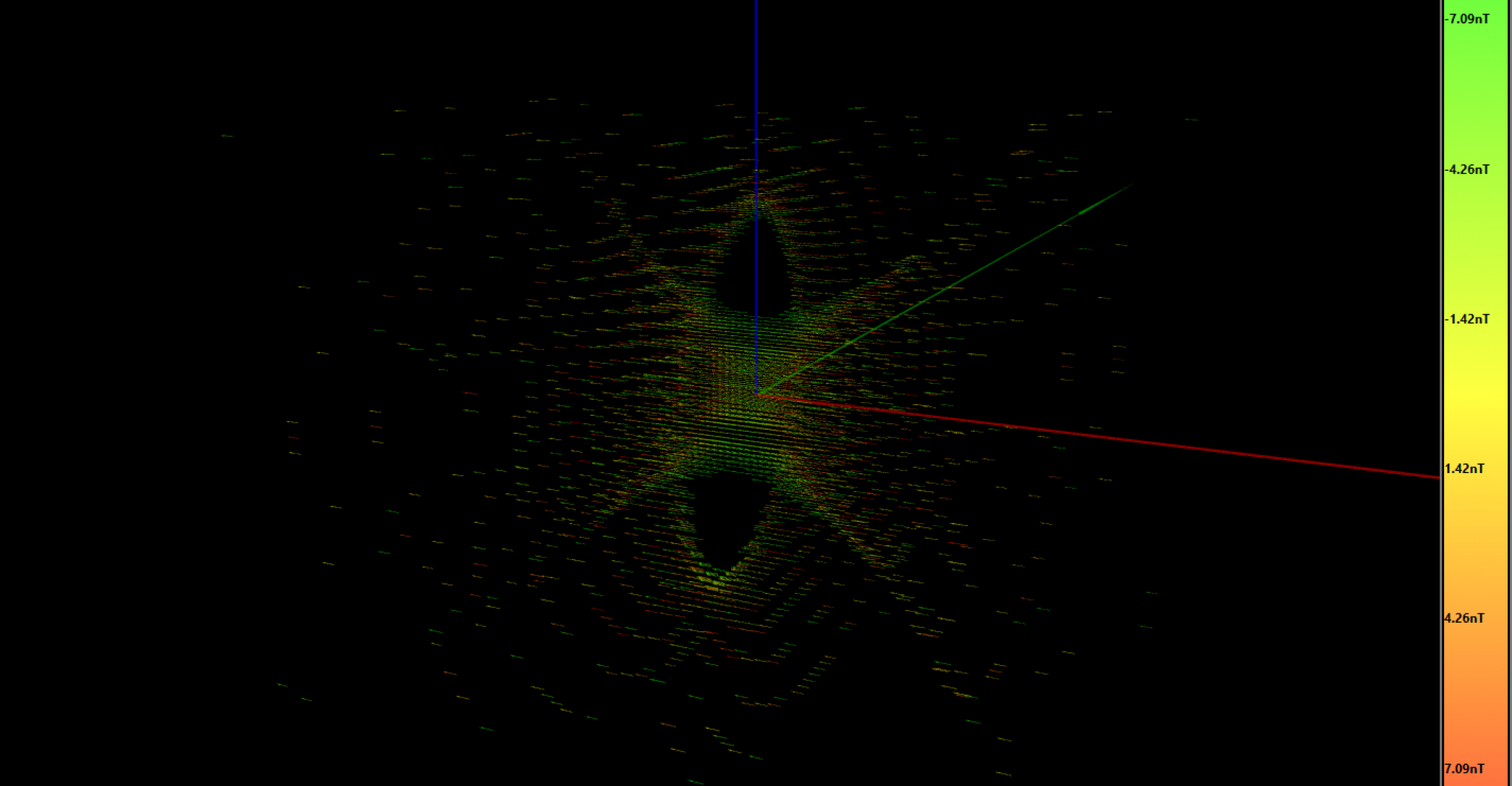
I coded the geometry and the current for each coil, according to the results of the Matlab script. As already said, we just calculate the magnetic field along the X-axis, so here we will see the final 3D result and the homogeneity volume. I made a video because it’s worth seeing in movement. The first simulation is for a 1mm grid, only showing the vectors falling inside the 2ppm region:
The vector count is 3341, which means that in this volume we have at least 3341mm³ (we can call them voxels) of 2ppm in magnetic homogeneity.
This second simulation is the same, increasing the homogeneity to 4ppm. The number of voxels now increased to 7267 (equivalent to 7.3cm³):
I haven’t uploaded the 6ppm video because it was quite similar to the previous one, but the zone increased up to 10171 voxels (10.2cm³). Not bad! Although I was expecting a higher volume.
The simulator took about 10 minutes to perform all the calculations, even using strategies in C# to run the code in all the 8 cores of my computer.
This information is very useful because now we can adjust the geometry of the RF coil to maximize the filling factor. We have about 4cm of diameter and 1.5cm of length where we have our most homogeneous magnetic field to get a useful image.
Finally, just as a matter of comparison, I designed a Helmholtz coil using the same technique. The Helmholtz coil has a separation between coils equal to the radius, but it’s only true when you have a few copper turns. As already seen before, adding more turns (in height or width) widens the shape of the resultant magnetic field, so the separation has to be adjusted to achieve the flattest curve at the center. I tried the results to be as much similar as possible to my design:
C1 Coil
Displacement=40.18mm
C1 Current= 630.1560 mA
C1 Coil Turns (1/2)= 706
C1 Total R (1/2)= 10.9933 ohm
C1 Wire Length (1/2)= 337.5348 m
C1 Coil Weight (1/2)= 1.5971 kg
C1 Voltage (1/2)= 6.9275 V
C1 Power (1/2)= 4.3654 W
Central Magnetic field: 5.084 mT
Larmor freq: 216.4761 kHz
Total Power: 8.7308W
Homogeneous space: 5.3309mm
Copper weigth: 3.2137kg
After running the simulation, only 591 elements were found (0.6cm³) in the 6ppm volume, in comparison with the 10.2cm³ we could achieve with our 5-coil approach. For its design I tried to achieve the same dissipated power (8.7W vs 8.4W) to get the same magnetic field. As you can see, I need about 2.1 times the total copper volume, but I achieve 17 times more homogeneity than in the Helmholtz coil, so I guess the extra copper is worth to be paid! 😛
For the video, instead of running the previously designed Helmholtz structure, I run the simplest Helmholtz form using only 2 thin conductors. The coils also separated 35mm instead of 40.2mm found to be better in the previous specific case. In this most generic case, only 291 volume elements (0.29cm³) were found in the 6ppm range. It has sense because the shape of the magnetic field is sharper than in wider coils:
As you could notice, in all these simulations it’s only shown half of the windings. It’s done on purpose to prevent the background coil to visually interfere, but of course in reality the copper will be there. That’s it for today!
Stay tuned!