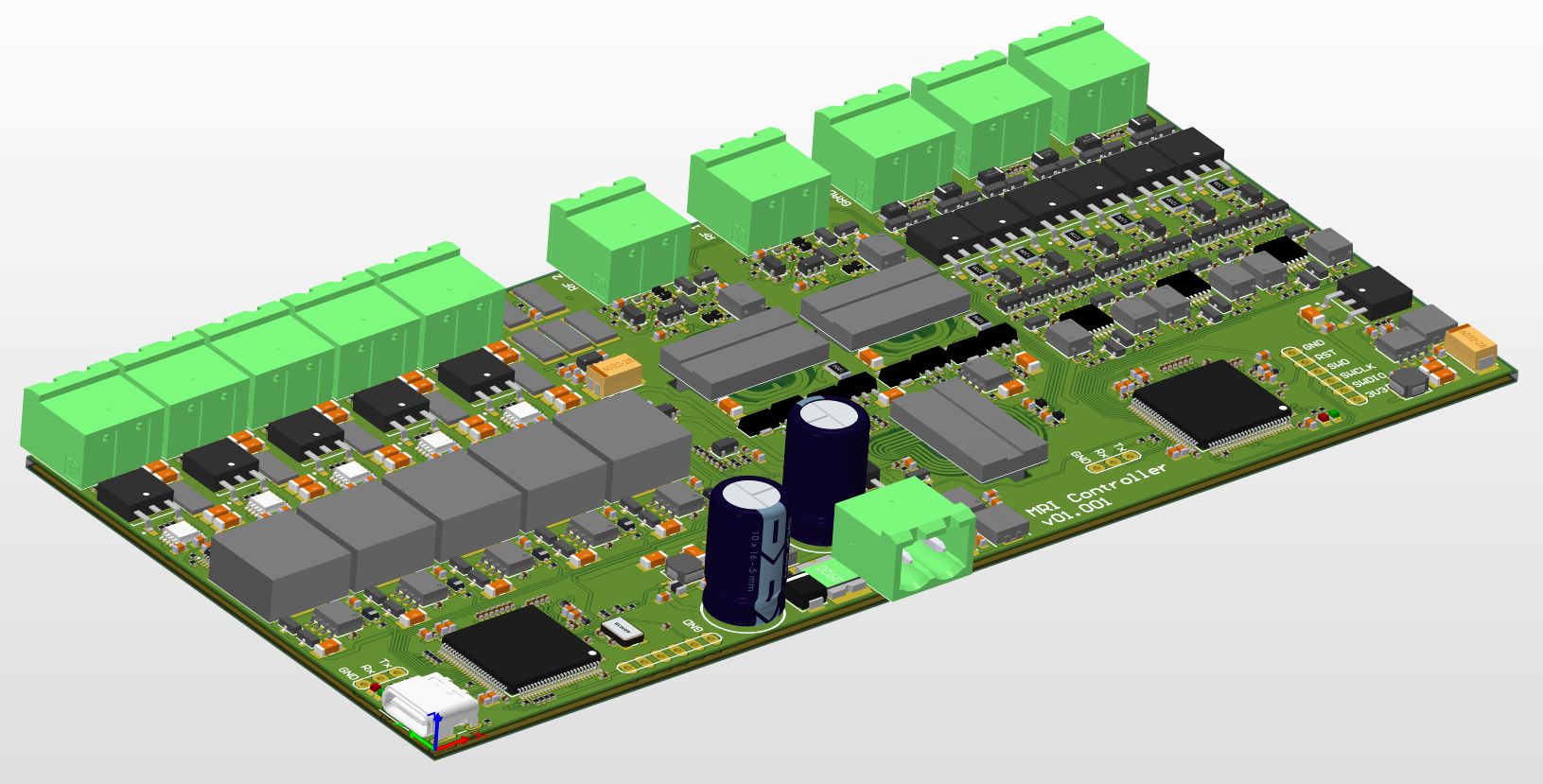
It took me about 2 weeks of work in my free time, but the PCB is finally finished! The main features:
- 5 independent channels of DCDC + linear current source to drive the 5 coils which generate the main B0 magnetic field. One 16-bit dual DAC per channel is used to configure the current setpoint, as well as generating an ultra-high precision 2.5V reference with low temperature drift and very low noise. Apart from using this reference for the current sources, the reference is spread through the board to be used as the main reference for the microcontroller’s ADCs, the signal amplifiers, the NTC sensor and the gradient coil drivers
- 2 independent drivers to generate the quadrature rotating magnetic field (RF field), as well as 2 amplifiers and all the logic to switch from transmitter to receiver. A third differential amplifier with some extra gain is used to remove the common mode noise and to acquire the NMR signal
- 3 independent drivers to generate the X, Y and Z gradient magnetic fields. The Z gradient field might not finally be used, since the simulations showed an homogeneity zone of just 1.5cm in the Z direction, but the driver will be there just in case
Two microcontrollers are used (STM32H7 family). The master is used to communicate with the computer through USB (USB 2.0 over a USB C connector) and to send commands to the slave. It also controls the PWMs of the 5 drivers to generate the B0 magnetic field, and to control each linear current source using each DAC (through SPI). It also measures the temperature using a NTC, thermally coupled to all the shunt resistors, and compensates the current setpoint when the shunt resistors temperature changes according to the temperature coefficient of each resistor, which was chosen as low as possible (100ppm/ºC).
The slave microcontroller is the one that performs the main MRI tasks. It generates both RF signals (the main and the 90º shifted one) using both internal DACs + DMA. It also controls the gradient magnetic field timings, and the integrated 16-bit ADC @ more than 5MSPS is used to capture the 210kHz signal.
PCB Layers:
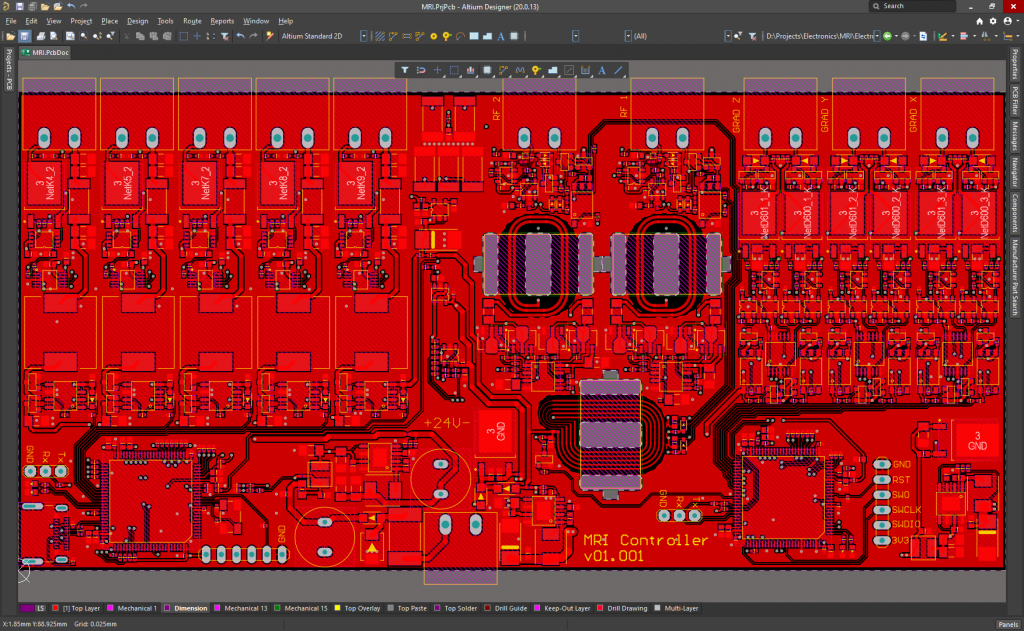
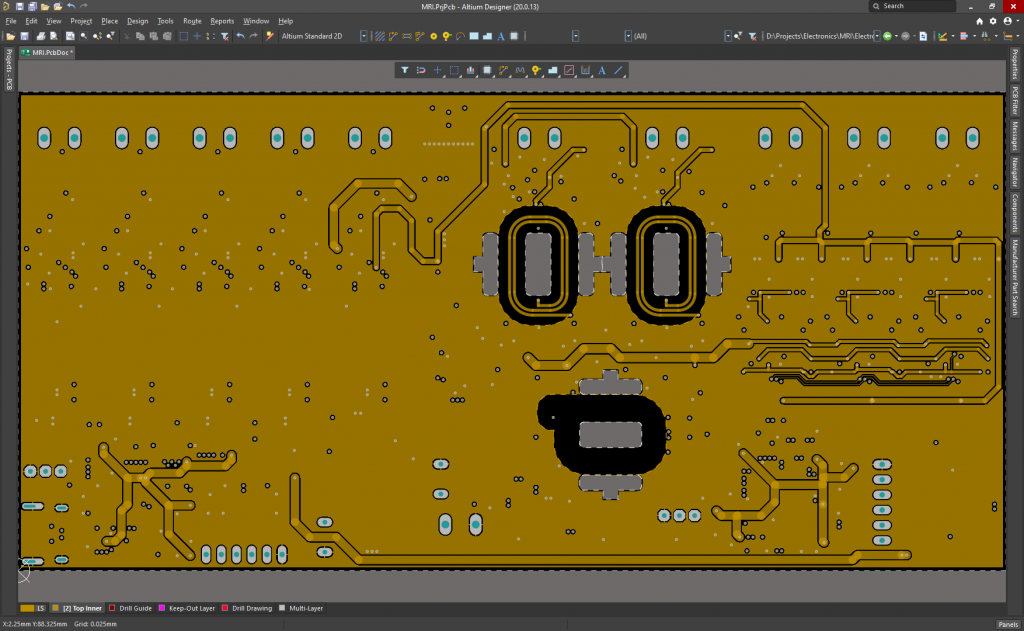
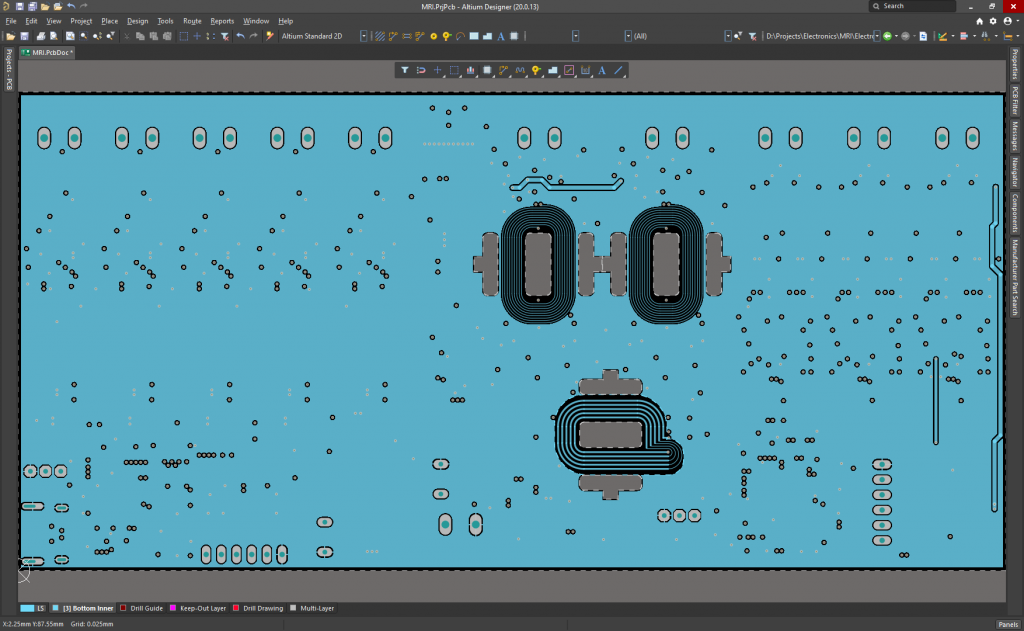
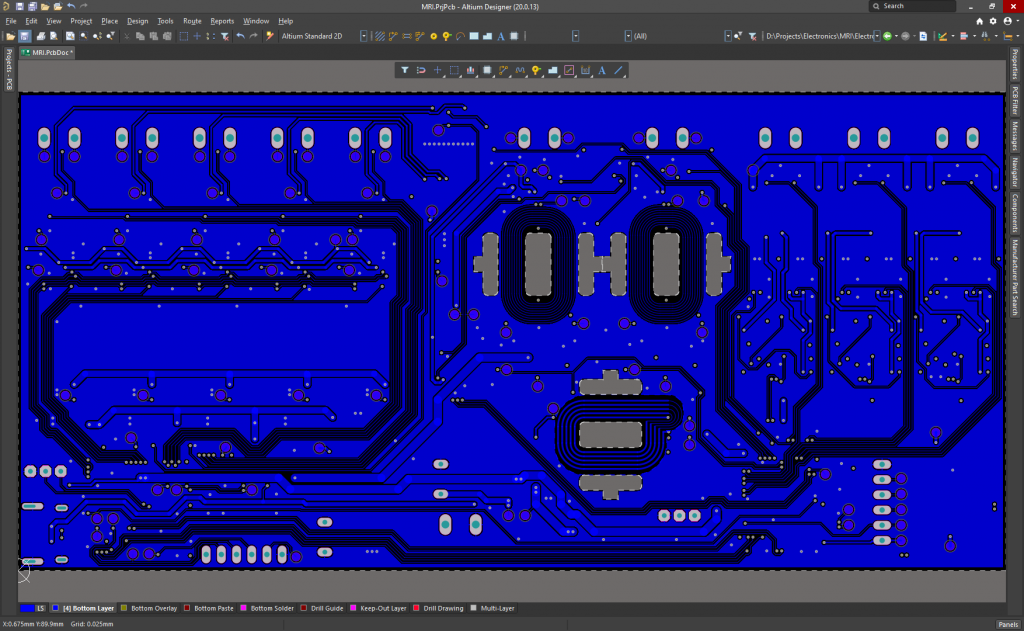
It is powered at 24V, although the microcontrollers can run and be programmed using the 5V of the USB C connector when plugged to the PC. It measures 165.2mmx80mm, and it has been ordered to Eurocircuits today.
I will assemble it next week, I’ll post the results soon!