The initial design with the PCB planar transformer gave quite bad results in terms of signal distortion. That’s why I decided to use one pulse transformer per quadrature channel.
This transformer is a 1:1:1 (meaning it has 3 independent and equal coils). I use the first coil to apply the signal, and connecting the other two in series I get an output voltage 2 times higher than the input.
The signal applied to the trasformer comes from an operational amplifier working at 24V, with a maximum output voltage span of about 2V to 22V. I use 2 operational amplifiers to transform the single DAC output voltage (from 0 to 2.5V) to a differential voltage of ±20V. With the extra 2x gain of the transformer, we get a total output voltage of 80VPP which can be directly applied to the RF coils.

Mesurement of the static RF coil magnetic field
To calculate the flip angle given by the RF pulse, we first must know the magnetic field generated by the RF coils (which using the common nomenclature, we will call B1). So I used a digital magnetometer. I know it’s not the most accurate way to do it, but it’s a good starting point. Once I get some NMR signal, we will be able to play with the flip angle to find the optimum value.
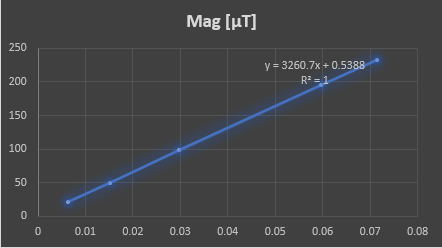
The magnetometer was placed in the middle of the RF coil. I used a STM32 eval board to get the magnetometer data using I2C, and send it to the PC using a USB VCP. Then I applied some different currents to the coil to get this table:
| IDC [A] | Mag [µT] |
| 0.00637 | 21 |
| 0.0152 | 50 |
| 0.0298 | 98 |
| 0.0595 | 195 |
| 0.0714 | 233 |
Now we just need to know the impedance of the coil at the NMR frequency. It’s important to measure it instead of just calculating it, because we also want to have into account the high frequency loses (like the proximity effect one). So I used a 216Ω shunt resistor to measure the current with the oscilloscope, and I applied 8.6VPP with the function generator. A simple V/I division gives an impedance of 6435Ω @ 213kHz.
Flip angle and flip time
The flip angle just depends on the time we apply the pulse and the magnitude of the applied magnetic field (B1). Here the equation:
![]()
Knowing that we can generate up to 80VPP, we can get the current of the coil from the previous calculated parameters:
![]()
Now, from the tendency line equation found out in the previous plot, we can find out the B1:
![]()
We now will use the peak magnitude instead of the peak to peak. It is clear why when we apply the common trick of switching to the rotating frame of reference, so that we now rotate with the nucleus and see a static magnetic field. The quadrature system with a sine/cosine signal will make that the nucleus sees a static and constant magnetic field with a magnitude equal to the peak value.
Note that to flip the spin angle to 90 degrees we are talking of only 20μT! This result was quite shocking to me, since it’s about half the earth magnetic field! I didn’t expect that…
Now we have all we need to calculate the flip time to get a 90 degree flip angle:
![]()
This time is equivalent to:
![]()
Quadrature signal
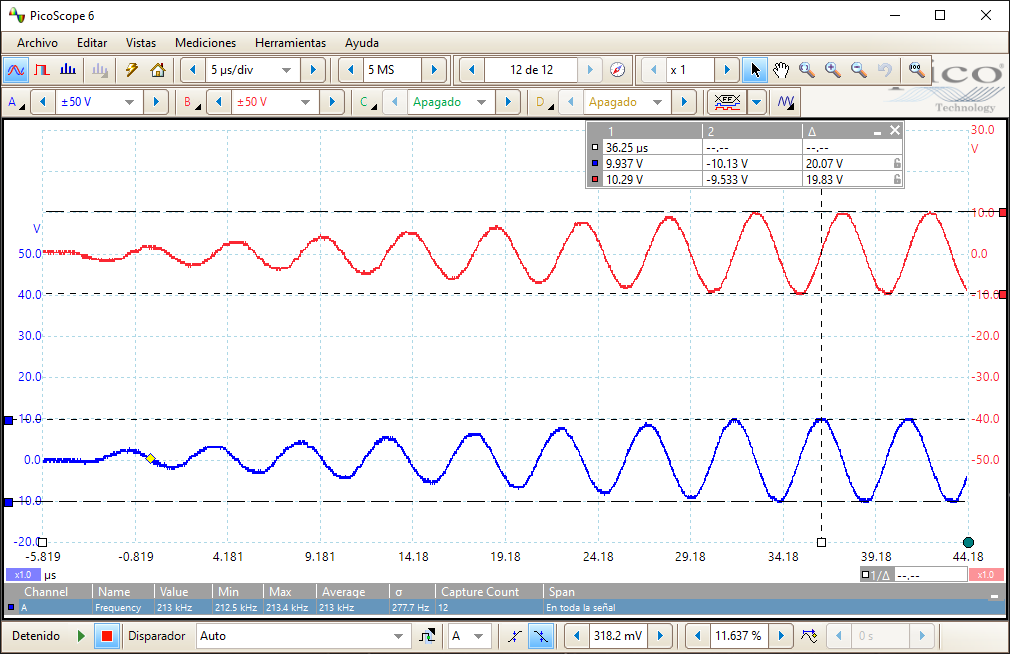
Here I show the oscilloscope capture of the 2 signals which are applied to the RF coils. They are generated with the internal DAC peripheral of the microcontroller, a DAC configured in dual mode (both channels updated at the same time) to send the signal to each channel. It’s actually the same signal, but shifted 90º to give the quadrature feature.
The signal shape is first calculated using a “for” loop, and stored in a RAM array. Then, using a timer, each data in the RAM array is transferred to the DAC using a DMA. The resultant signal is very smooth, since I’m running the DAC at 5MSPS to generate the 213kHz. All this process is already generated inside the microcontroller, but I have some programming work to do to control everything from the computer.